Quant Interviews & Essential C++ Questions You Must Know

AlgoQuantHub Weekly Deep Dive

Author

Nicholas Burgess
September 19, 2025

Welcome to the Deep Dive!

Here each week on ‘The Deep Dive’ we take a close look at cutting-edge topics on algo trading and quant research.

Last week, we turned to the world of American options, putting pricing theory to the test against live markets and option chain quotes on Interactive Brokers (IBKR). This week, we discuss the quant interview process and the essential C++ questions you must know.

Bonus content, we discuss the hidden agenda behind interview questions on trivial functions such as Fibonacci series, where we are expected to discuss and demonstrate an understanding of time space complexity and ‘Big O’ notation.

Table of Contents

Exclusive Algo Quant Store & Discounts

Get 25% off all purchases at the Algo Quant Store with code 3NBN75MFEA

Feature Article: Essential C++ Interview Questions

Interviewing for quant roles at hedge funds and investment banks is notoriously demanding—requiring a rare blend of advanced programming ability, mathematical rigor, and financial intuition. Many candidates, even highly experienced ones, struggle to make it through the process: the estimated failure rate for quant interviews can be as high as 90%. This is not a reflection of talent, but of how competitive and selective the field is. The key is to approach these interviews with resilience—failure is the norm, not the exception. Every attempt builds knowledge and sharpens your skills, and persistence is often the difference between rejection and eventual success.

To help with the preparation and interview process below are five of the most essential questions that frequently appear on C++ coding tests and technical interviews,

  1. Explain Object-Oriented Programming (OOP) and its Pros and Cons
    OOP is a programming paradigm built on four pillars: abstraction, encapsulation, inheritance, and polymorphism. Abstraction allows developers to hide complexity, encapsulation groups related data and behaviours into objects, we reuse and extend code via inheritance, and we customize methods to for different objects through polymorphism. OOP makes complex systems modular and easier to maintain but can introduce overhead and complexity if misused. For further information on OOP, see Code Institute’s OOP Overview and DesignGurus Beginner's Guide to OOP.

  2. What is a Smart Pointer? How Would You Implement One?
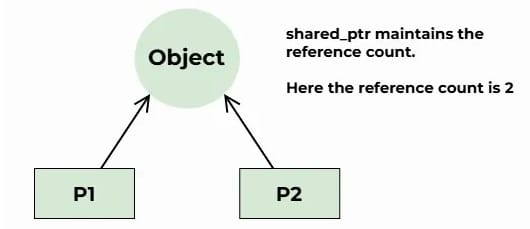
    Memory safety and efficient management are pillars of robust C++ in quant roles. Smart pointers like unique_ptr and shared_ptr automate resource management to avoid Implemented as a class they behave like a regular pointer but they also manage ownership and automatically free dynamic memory when no longer needed. This prevents common issues such as memory leaks and dangling pointers. The most common approach is reference counting: each smart pointer constructor increments an instance counter when it shares ownership of an object, and when one goes out of scope, the destructor decrements this instance counter; once it reaches zero, the resource is deleted. memory leaks. For more details, see C++ Smart Pointers on cppreference and Fluent C++ on Rule of Three and GeeksforGeeks Smart Pointers.

  3. Describe Stack, Heap, and Static Variable Storage in C++
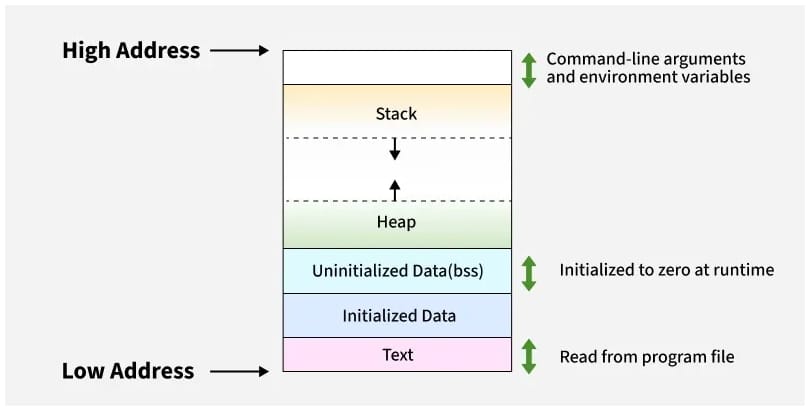
    Memory layout questions test your understanding of low-level systems and are crucial for building reliable, high-performance quant applications: the stack stores local variables and function calls, offering fast allocation and automatic cleanup when a function ends; the heap manages dynamic allocations made with the new operator, allowing persistence beyond the current scope but requiring explicit cleanup with delete or smart pointers; and static variables, whether global or function-local, reside in the data segment, where they are initialized once and retain their value throughout the entire lifetime of the program, providing global persistence. For a deeper understanding, see CppReference on Storage Duration and GeeksforGeeks Memory Layout.

  4. Explain Quick Sort vs Bubble Sort: Time and Space Complexities
    Bubble Sort and Quick Sort are both comparison-based algorithms but differ greatly in efficiency. Bubble Sort repeatedly swaps adjacent elements so the largest “bubbles up” to the right with each pass. It runs in O(n2) time on average and in the worst case, with O(1) space, making it simple but inefficient on large datasets. Quick Sort instead chooses a pivot and partitions the array into smaller and larger values placed left and right of it. Often the rightmost element is chosen as the pivot; each partition step puts the pivot into its correct sorted position. Quick Sort averages O(nlog⁡n) time, has a worst case of O(n2) with bad pivots, and uses O(log⁡n) space for recursion. In short, Bubble Sort is slow and brute-force, while Quick Sort is much faster and widely used in practice. For diagrams and detailed complexity analysis, see Visualgo Quick Sort and GeeksforGeeks Bubble Sort.

  5. What is the Rule of Three and Rule of Five in C++? Why Are They Important?
    This question tests your understanding of resource management and object lifecycle in C++. The Rule of Three in C++ states that if a class defines any one of the following—a destructor, a copy constructor, and an assignment operator—it should explicitly define all three. This is because such classes usually manage resources that require careful copying and cleanup to avoid issues like memory leaks or double deletions. With the introduction of move semantics in C++11, this rule expanded to the Rule of Five, which adds the move constructor and move assignment operator to the list. These rules are important because they help maintain exception safety, resource management, and prevent bugs in classes that handle dynamic memory or other resources. or a full explanation, see CppReference Rule of Three/Five and Stack Overflow explanation.

Keywords:
C plus plus, C++, essential knowledge, object orientated programming, OOP, Smart Pointer, Shared Pointer, Memory Management, Stack, Heap, Data Segment, Static Variables, Quick Sort, Bubble Sort, Big O Notation, Space Complexity, Time Complexity

Bonus Content: Fibonacci Series, Time Space Complexity & Big O Notation

The Fibonacci series is a famous sequence in mathematics and computer science. It starts with 0 and 1, and every subsequent number is the sum of the two preceding numbers:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

This simple yet elegant sequence is a cornerstone example to evaluate algorithmic thinking, recursion, iteration, and advanced optimization methods during interviews.

Recursive Approach
The recursive solution mirrors the Fibonacci definition straightforwardly:

int fibonacci(int n)
{
    if (n <= 1) return n;
    return fibonacci(n-1) + fibonacci(n-2);
}

While elegant, recursive calls quickly explode exponentially. The function recomputes many values repeatedly, leading to a time complexity of O(2n). The space complexity is O(n) from the recursion stack. This approach becomes inefficient with even moderately large n.

Iterative Approach
A practical and efficient solution uses iteration. It stores only the last two Fibonacci numbers and computes the sequence up to n:

int fibonacci(int n)
{
    if (n <= 1) return n;
    int prev1 = 0, prev2 = 1, curr;
    for (int i = 2; i <= n; ++i)
    {
        curr = prev1 + prev2;
        prev1 = prev2;
        prev2 = curr;
    }
    return curr;
}

This approach runs in linear time O(n) and uses constant space O(1), making it ideal for most applications.

Matrix Exponentiation: The Fastest Method
To compute Fibonacci numbers efficiently for very large n, we can use the matrix exponentiation method. We express Fibonacci numbers using matrix exponentiation with the equation:

Given the initial values of the Fibonacci series F1 = 1 and F0 = 0, this can be simplified to:

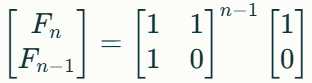
By raising the matrix to the (n−1)th power using fast binary exponentiation, we efficiently compute the nth Fibonacci number in the top-left element of the resulting matrix-vector product. This method considerably reduces the time complexity to O(logn), compared to O(n) for iterative and O(2n) for naive recursion.

#include <iostream>
#include <array>
using namespace std;
using Matrix = std::array<std::array<long long, 2>, 2>;

// Multiply two 2x2 matrices A and B
Matrix multiply(const Matrix& A, const Matrix& B)
{
    Matrix result = {{{0, 0}, {0, 0}}};
    for (int i = 0; i < 2; ++i)
        for (int j = 0; j < 2; ++j)
            for (int k = 0; k < 2; ++k)
                result[i][j] += A[i][k] * B[k][j];
    return result;
}

// Compute matrix exponentiation using fast exponentiation (squaring)
Matrix matrixPow(Matrix base, long long n)
{
    Matrix result = {{{1, 0}, {0, 1}}}; // Identity matrix
    while (n > 0)
    {
        if (n & 1) // If n is odd, multiply the result by base
            result = multiply(result, base);
        base = multiply(base, base); // Square the base
        n >>= 1; // Divide n by 2
    }
    return result;
}

// Calculate the nth Fibonacci number using matrix exponentiation
long long fibonacci(long long n)
{
    if (n == 0) return 0; // Base case for Fibonacci(0)
    Matrix base = {{{1, 1}, {1, 0}}}; // Transformation matrix
    Matrix result = matrixPow(base, n - 1); // Raise matrix to power n-1
    return result[0][0]; // Top-left element is fib(n)
}

int main()
{    
    // Example usage
    for (int i = 0; i<=50; ++i)
    {
        printf("%s%d%s%lld\n", "fib(", i, "): ", fibonacci(i));
    }
    return 0;
}

This approach is powerful for large n and exemplifies how understanding linear algebra and efficient algorithms can drastically optimize classical problems.

Keywords
Fibonacci Series, Sequency, Recursive Approach, Iteration, Matrix Exponentiation, Time and Space Complexity, Big O Notation, C++ C plus plus, Efficiency, Speed, Performance, Low Latency

Feedback & Requests

I’d love your feedback to help shape future content to best serve your needs. You can reach me at [email protected]