• AQH Weekly Deep Dive
  • Posts
  • Option Pricing Explained: Replication, Martingales & Risk-Neutral Pricing (In Plain English)

Option Pricing Explained: Replication, Martingales & Risk-Neutral Pricing (In Plain English)

AlgoQuantHub Weekly Deep Dive

Author

Nicholas Burgess
October 17, 2025

Welcome to the Deep Dive!

Here each week on ‘The Deep Dive’ we take a close look at cutting-edge topics on algo trading and quant research.

Last week, we shift focus from investment opportunities to risk management, exploring how professionals structure portfolios to capture upside while safeguarding against catastrophic drawdowns. This week, we dive into and demystify the fundamental mechanics of option pricing models, explaining how replication, martingale, and risk-neutral concepts drive option values and guide decisions on the optimal exercise timing—which is critical for successful options trading.

Bonus Content: Option Pricing Resources for Live Trading
For readers ready to take their understanding further, this week’s bonus content introduces the best resources for mastering option pricing models for live trading, explaining replication, martingale, and risk-neutral concepts in depth and in plain English to make complex theory accessible without compromise. You’ll find links to top-tier video tutorials, interactive spreadsheets, and professional software tools—all designed to let you test, implement, and adapt strategies in practice. These materials have been successfully and profitably applied in live trading, bridging theory and actionable results, and provide everything you need to deepen your knowledge, experiment in Excel, and explore professional-grade tools that help you understand, apply, and profit from the principles behind option pricing and optimal exercise.

Table of Contents

Exclusive Algo Quant Store & Discounts

Algo Trading & Quant Research Hub
Get 25% off all purchases at the Algo Quant Store with code 3NBN75MFEA

Feature Article: Understanding Option Pricing Mechanics

At the heart of modern option pricing lies a deceptively simple idea: if you can replicate an option’s payoff using traded assets, you can determine its fair value without guesswork. This is the principle of replication. Imagine holding a combination of stock and cash that perfectly mirrors the payoff of an option at every point in the future. The cost of creating that portfolio must equal the value of the option today—otherwise, arbitrageurs could lock in risk-free profit.

To construct a replicating portfolio, we hold Δ units of stock S and invest or borrow φ in a savings account B that grows at the risk-free rate with B(t) = exp(r t). The total portfolio value is:

V(t) = Δ(t) S(t) + φ(t) B(t)

If no external funds are added or withdrawn, the portfolio is self-financing, meaning all changes in value come solely from the movements of the underlying assets. This ensures the replicating portfolio evolves in lockstep with the option, creating a no-arbitrage condition that pins down the option’s price.

A crucial concept in this framework is the numeraire—the benchmark asset used to fund or measure the replicating portfolio. The choice of numeraire determines both the units of valuation (USD, EUR, or even units of stock) and the pricing probability measure, which governs the expected growth of both the numeraire and the replicating portfolio. When the numeraire is a risk-free savings account, the associated probability measure is called the risk-neutral measure (Q). Under this measure, both the savings account and the replicating portfolio grow at the risk-free rate.

By discounting the replicating portfolio or asset by the numeraire, we remove predictable growth. This gives rise to the martingale property, a central result in option pricing:

The expected discounted value of a future payoff, when discounting by the numeraire, equals the current value of the asset or portfolio.

Mathematically, when using the Q-measure we write this as,

E^Q [ exp(-r t) S(t) ] = S(0)

Where:

  • E^Q[…] denotes the expected value under the risk-neutral measure Q.

  • exp(-r t) is the discount factor for time t at the risk-free rate.

  • S(0) is the current price of the asset.

Key Concepts:
In plain terms, the expected discounted payoff equals today’s price. Once we remove predictable growth at the risk-free rate, the discounted asset or portfolio has no drift, its expected value equals the current price, and it is a martingale.

  • Replicating Portfolio Approach: Solve for Δ and φ at each node in a binomial tree so the portfolio exactly matches the option payoff. The current cost of the portfolio gives the option price.

  • Risk-Neutral / Probability Approach: Compute the discounted expected payoff under Q. The price is obtained without explicitly constructing Δ and φ. The existence of a self-financing portfolio guarantees that this measure exists and the pricing is consistent.

Both approaches are mathematically equivalent. A replicating portfolio guarantees the existence of a risk-neutral measure and enforces no-arbitrage pricing.

Applications in Practice
The following examples highlight the power of the martingale approach: by discounting and taking expectations under Q, we remove predictable growth and isolate the pure, risk-adjusted uncertainty that drives option values. This reasoning applies not just to American options, but to virtually every derivative instrument in modern finance.

1. Monte Carlo Simulation for European Option Pricing:
Simulate many future price paths under the risk-neutral measure Q. Compute the expected value by taking the average of discounted payoffs along all paths. The martingale property ensures this reflects the option’s fair value today giving,

V(0) ≈ Average [ exp(-r T) Payoff(S_T) ]

Where S_T is the simulated asset price at expiry and Payoff(S_T) is the option payoff along each path.

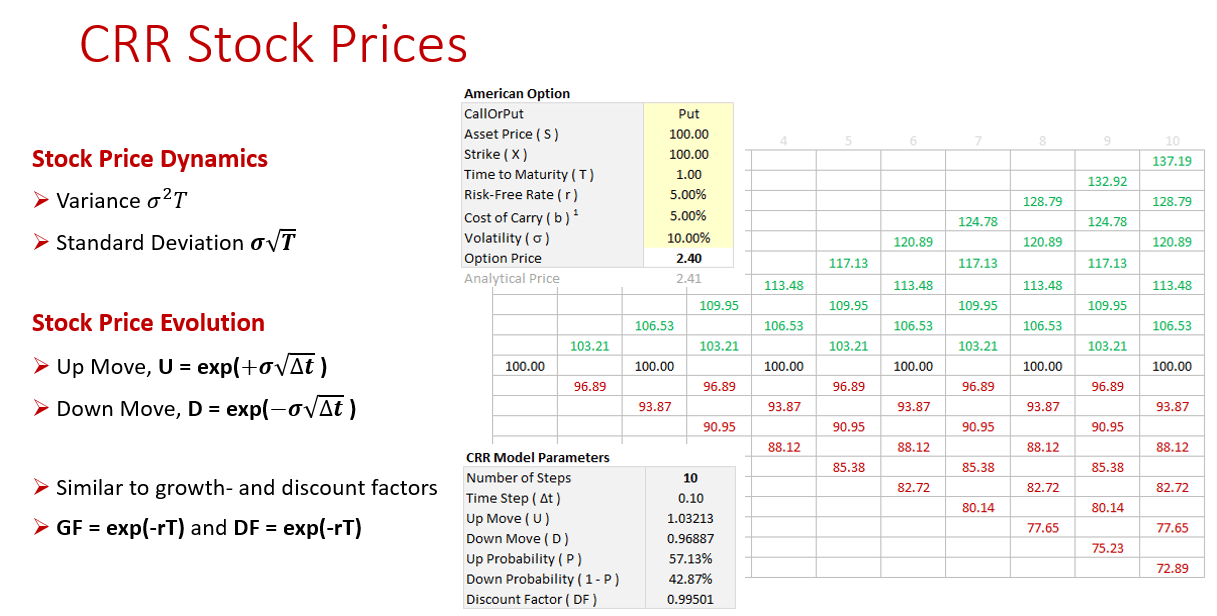
2. Binomial Trees for American Option Pricing:
Construct a binomial tree and compute the expected value at each node as the discounted average of successor node values under risk-neutral probabilities p. This step-by-step approach enforces the martingale property and gives the option price at each node as,

V(t) = exp(-r Δt) [ p V(up) + (1 - p) V(down) ]

3. Interest Rate Swaps (Terminal Forward Measure):
Use a discount bond maturing at T as the numeraire. Discount fixed and floating leg payments back to today. The expected value under the T-forward measure exists in principle but vanishes because the discounted floating leg is deterministic:

Swap Value = Σ [ discounted fixed payments ] - Σ [ discounted floating payments ]

4. FX and Commodity Derivatives:
Select an appropriate numeraire (foreign savings account, commodity forward, or stock). Compute the expected value of discounted payoffs under the numeraire measure. This ensures consistent pricing of forwards, options, and multi-asset derivatives.

Key Takeaways:

  • The self-financing replicating portfolio is the conceptual backbone of option pricing.

  • Choosing a numeraire and measure lets us manipulate expected growth mathematically.

  • Discounting under the numeraire gives the martingale property, allowing direct computation of option prices without explicitly solving for Δ and φ.

  • Both replicating portfolio and risk-neutral expectation approaches are equivalent; understanding the equivalence is a core insight in quantitative finance.

Further Reading:

  1. Hull, John. Options, Futures, and Other Derivatives – Chapters on replication and risk-neutral pricing.

  2. Shreve, Steven. Stochastic Calculus for Finance II – Detailed derivations of martingales and Q-measure applications.

  3. Cox, Ross, Rubinstein (1979), Option Pricing: A Simplified Approach – Binomial tree intuition.

  4. Wilmott, Paul. Paul Wilmott on Quantitative Finance – Practical applications and modeling.

  5. Musiela & Rutkowski. Martingale Methods in Financial Modelling – Advanced martingale theory.

Keywords:
option pricing, replication portfolio, self-financing, numeraire, risk-neutral measure, martingale property, delta hedging, Monte Carlo simulation, binomial tree, derivatives, American options, FX derivatives, interest rate swaps, quantitative finance, financial mathematics

Bonus Content: Option Pricing Resources for Live Trading

For readers ready to take their understanding further, this week’s bonus introduces the best resources for mastering option pricing models for live trading. We explain replication, martingale, and risk-neutral concepts in depth—and in plain English—making complex theory accessible without compromise. You’ll find links to top-tier video tutorials, interactive spreadsheets, and professional software tools—all designed to let you test, implement, and adapt strategies in practice. These materials have been successfully applied in live trading, bridging theory and actionable results.

1. YouTube Video - Options Pricing Optimal Exercise
Includes section on self-replicating portfolios, martingales, risk-neutral pricing and how to price American options using CRR trees.

2. Excel Workbook - Cox, Ross & Rubenstein Model for Option Pricing
The support workbook for the video item 1. A dynamic workbook giving a full breakdown of how to implement the CRR model for American option pricing and incorporate optimal exercise.

Additional Training Resources: Live Options Trading, Pricing & Risk

Take your understanding from theory to practice with our YouTube training series and premium Excel workbooks. These hands-on resources walk you through live option pricing, risk management, and trading strategies used by professional traders. Each model is built for real-market application, helping you visualise payoff structures, Greeks, and risk-reward dynamics in real time. Whether you’re refining your quant skills or developing your own automated trading system, these materials give you the edge to trade options with confidence and precision.

3. YouTube Playlist - Live Option Trading Videos
A four-part video series covering Live European and American options trading: 1. Live Options Trading, 2. Trading Strategies, 3. Pricing Theory and Optimal Exercise, 4. Live Option Pricing in Excel and how to match IBKR market prices.

4. American Option Pricing Workbook - Live Pricing, Risk & Trading Strategies
An extensive Excel workbook, showing how to price live European and American options, how to compute risk and how to create popular live trading strategies and match IBKR live market prices.

5. Premium Content - Options Training Bundle
A full comprehensive options training bundle with YouTube video support.

Feedback & Requests

I’d love your feedback to help shape future content to best serve your needs. You can reach me at [email protected]