Monte Carlo Pricing & Fast Convergence using Sobol Brownian Bridge

AlgoQuantHub Weekly Deep Dive

Author

Nicholas Burgess
November 28, 2025

Welcome to the Deep Dive!

Here each week on ‘The Deep Dive’ we take a close look at cutting-edge topics on algo trading and quant research.

Last week, we looked at FX options and the world of volatility smiles — showing how traders turn deltas, risk reversals, and butterflies into a full smile that reveals the market’s view of currency moves.

This week, we explore how Monte Carlo with quasi-random number Sobol sequences and Brownian Bridge results in option pricing that converges dramatically faster than traditional pseudo-random simulation.

Bonus Content, here show how to generate Sobol Brownian Bridge random numbers, giving a practical coding example in C++ using the QuantLib open source library.

Table of Contents

Exclusive Algo Quant Store & Discounts

Algo Trading & Quant Research Hub
Just for today - Enjoy Black Friday with a massive 50% off with code: 2ZKDYNB0TO

Feature Article: Faster Monte Carlo Convergence with Sobol Brownian Bridge

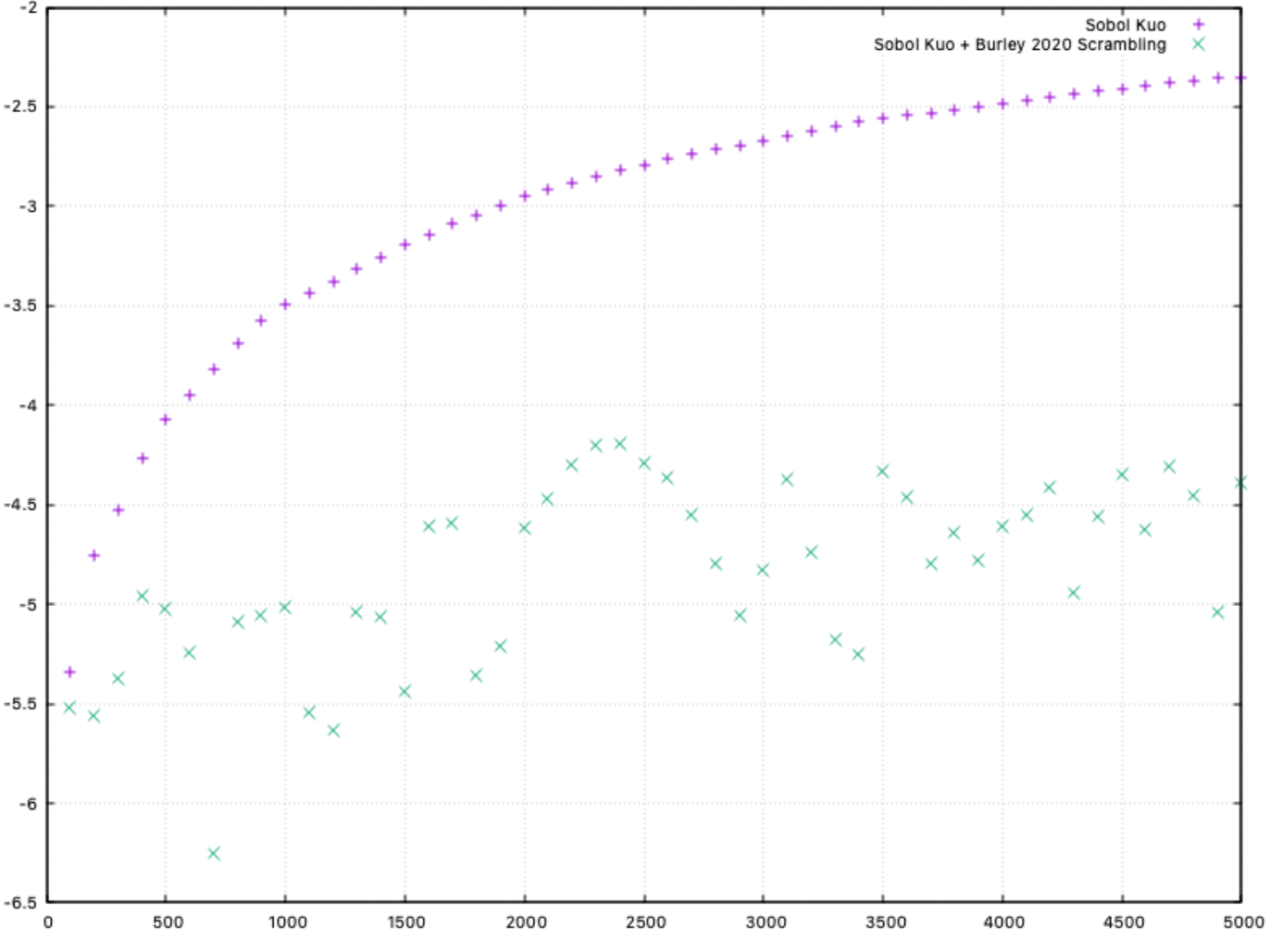
Classic Monte Carlo draws random numbers using pseudo random number schemes such as Mersenne Twister that look statistically correct, however they often cluster together and as a result they converge slowly to a solution. Quasi-Monte Carlo (QMC) replaces this wandering with deliberate even coverage of the sample space. Sobol sequences are low-discrepancy point sets, meaning they fill the space evenly and methodically, reducing clustering and voids. In numerical integration terms, that translates into smaller error and visibly smoother convergence of option prices.

Empirical tests also show that scrambled Sobol sequences can outperform standard Sobol, further improving convergence behaviour, as demonstrated in QuantLib’s research notes.

Brownian Bridge takes this further. Instead of generating a stochastic path sequentially in time (from today to maturity), it constructs the path hierarchically. The final point at maturity is generated first, then intermediate points are filled in conditionally. This re-ordering pushes the most important source of variance — the terminal value — to the earliest Sobol dimensions where low-discrepancy accuracy is strongest. The result is a path that respects Brownian motion statistics while exploiting the structure of Sobol sampling.

Mathematically, for two known points of Brownian motion W(t_i​) and W(t_j), the value at an intermediate time t_k is:

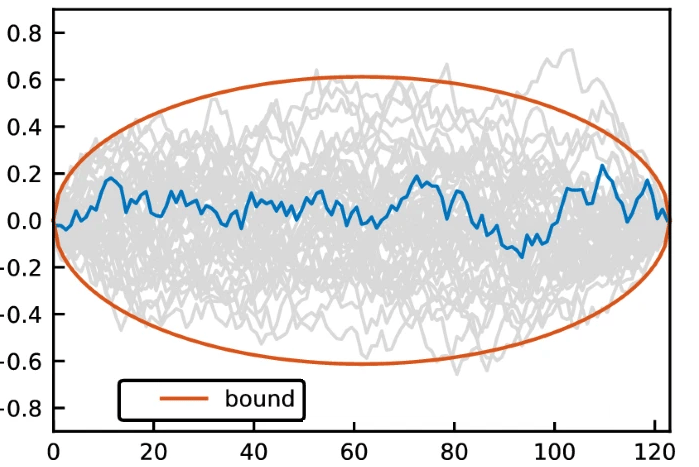
The practical consequence is that fewer paths are needed to achieve the same accuracy, and pricing curves stabilise early instead of over-oscillating. For European options, this can mean convergence improvements of orders of magnitude. When implemented carefully, Sobol Brownian Bridge turns Monte Carlo from a statistical hammer into a scalpel.

Correlation does affect ordering. Since Sobol sequences depend on assigning early dimensions to the most influential sources of randomness, correlation across assets can mix these influences. Professionals manage this either by applying correlation after the bridge (via Cholesky) or rotating the system with PCA so principal risk factors align with early Sobol dimensions. The objective remains sacred: concentrate variance where Sobol is most precise.

Finally, while European options benefit directly and cleanly from Sobol Brownian Bridge, more complex derivatives require additional discipline. Path-dependent products are highly sensitive to time discretisation choices, American options introduce numerical fragility through regression error in Longstaff–Schwartz, and barrier options risk mispricing if barriers are hit and retrace between discretization points, necessitating Brownian Bridge corrections or conditional sampling schemes. None of these challenges diminish the power of Sobol or the Brownian Bridge — they simply required informed use, design and careful implementation.

Recommended Reading:

Keywords:
Monte Carlo, Option Pricing, Price Convergence, Random Numbers, Pseudo vs Quasi, Sobol Sequence, Brownian Bridge, Low Discrepancy, Financial Engineering

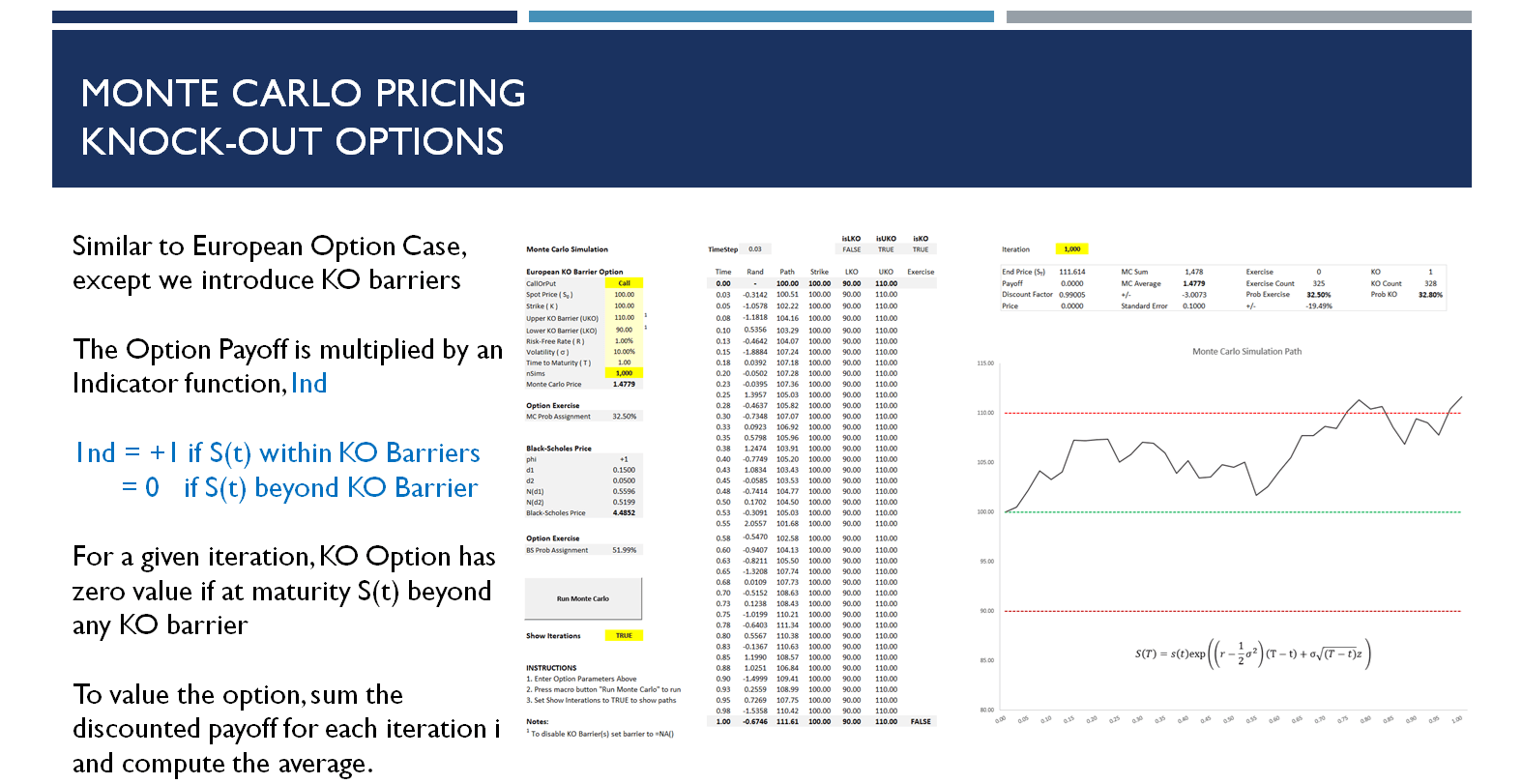
Feature Video: Monte Carlo Simulation

Professional Training & Excel Workbook
Monte Carlo Simulation for Option Pricing

Bonus Article: Generating Sobol Brownian Bridge Random Numbers in QuantLib

Here we present a QuantLib example in C++ that generates Gaussian-distributed random numbers using Sobol sequences and reorders them via Brownian Bridge. The pure stochastic backbone used by high-performance Monte Carlo engines.

These output values are Gaussian-distributed but ordered by importance according to Brownian Bridge construction, perfectly suited for constructing low-variance Monte Carlo paths. This is the same conceptual engine that quietly powers industrial-grade pricing systems.

QuantLib Documentation:
Low-discrepancy generators and Brownian Bridge using QuantLib.

#include <ql/quantlib.hpp>
using namespace QuantLib;


int main() {


Size steps = 8; // number of time steps
Size seed = 12345; // reproducibility


SobolRsg sobol(steps, seed);
InverseCumulativeNormal invNorm;
BrownianBridge bridge(steps);


Array sobolUniforms = sobol.nextSequence().value;
Array gaussian(steps);
Array bridgePath(steps);


// Convert Sobol uniforms to normal variates
for (Size i = 0; i < steps; ++i)
   gaussian[i] = invNorm(sobolUniforms[i]);


// Apply Brownian Bridge ordering
bridge.transform(gaussian.begin(), gaussian.end(), bridgePath.begin());


// Output Sobol Brownian Bridge numbers
for (Size i = 0; i < steps; ++i)
   std::cout << bridgePath[i] << std::endl;


return 0;
}

Keywords:
QuantLib, Sobol Brownian Bridge, Quasi Random Numbers, Monte Carlo C++, Gaussian Paths, Low Discrepancy Simulation

Feedback & Requests

I’d love your feedback to help shape future content to best serve your needs. You can reach me at [email protected]