FX Volatility Smiles & Market Quotes

AlgoQuantHub Weekly Deep Dive

Author

Nicholas Burgess
November 21, 2025

Welcome to the Deep Dive!

Here each week on ‘The Deep Dive’ we take a close look at cutting-edge topics on algo trading and quant research.

Last week, we discussed statistical inference and the logic behind hypothesis testing, p-values, Type I/II errors, and how these tools help us separate genuine edges from random noise and how to incorporate them into mean reverting and statistical arbitrage trading strategies.

This week, we dive into FX options and the world of volatility smiles — showing how traders turn deltas, risk reversals, and butterflies into a full smile that reveals the market’s view of currency moves.

Bonus Content, Ever wondered how traders turn a few market quotes into a full FX volatility smile? In this week’s bonus article, we break down the practical steps: from ATM vols, risk reversals, and butterflies to wing volatilities, and finally converting deltas into strikes using premium-adjusted conventions with formulas and a Python example you can try yourself.

Table of Contents

Exclusive Algo Quant Store & Discounts

Algo Trading & Quant Research Hub
Get 25% off all purchases at the Algo Quant Store with code 3NBN75MFEA

Feature Article: How FX Traders Build the Volatility Smile

The FX options world runs on a very particular language: deltas, risk reversals, butterflies, forward-moneyness and volatility smiles quoted at fixed deltas rather than fixed strikes. Traders do this because FX markets are fundamentally two-currency interest-rate worlds, where forwards are the “natural” anchor point. When you work in forwards, deltas give a cleaner sense of where an option sits on the distribution. Once you tune your ear to this dialect, the smile becomes much easier to interpret.

The famous FX volatility smile emerges because the market assigns different probabilities to tail events than the log-normal Black model assumes. When traders quote a 25-delta call, they’re quoting the implied vol of the strike whose forward delta equals +25%. A 25-delta put has a delta of –25%. These deltas can be premium-adjusted, meaning the delta is reduced by the sensitivity of the premium to the underlying. FX markets use premium-adjusted deltas for hedging because they more accurately reflect the spot-sensitivity you’re left with after paying for the option. The smile you see on a dealer page is built entirely from these conventions.

Risk reversals (RR) and butterflies (BF) are the core inputs. The RR measures directional skew — the implied vol difference between call and put wing. Butterflies measure curvature — how much extra convexity the smile has versus a flat line. When you add the ATM volatility, these three quotes fully determine the vols for the 25-delta and 10-delta call and put wings. This decomposition keeps quoting consistent across maturities and currency pairs, and lets dealers keep their risk books tidy.

Once you’ve turned RR/BF/ATM into implied vols at each wing, converting delta to strike is the crucial step. This requires using the appropriate delta convention (spot delta, forward delta, or premium-adjusted delta). Premium-adjusted delta tends to be preferred for spot hedging and risk books because it correctly accounts for the fact that option buyers fund the premium upfront. The moment you convert those deltas to strikes, your smile becomes a true volatility curve in strike space and can be plotted, interpolated, and used for pricing exotic instruments.

After the smile is built in strike space, you can stack the curves by maturity to build a full volatility surface. Once you have that, you can perform arbitrage-free smoothing, apply SABR or SVI fitting, and interpolate to any strike/maturity you need. This is where quant craft becomes art — no two banks build and smooth their surfaces exactly alike, and these details profoundly affect exotic option pricing, forward skew, and the dynamics that traders hedge against. The surface is the trader’s map of the future.

Recommended Reading:

Keywords:
fx options, volatility smile, volatility surface, delta convention, premium adjusted delta, spot delta, forward delta, risk reversal, butterfly, rr bf quotes, atm vol, fx derivatives, quant finance, fx trading, vol construction, implied volatility, exotic options, sabr, svi, delta to strike

Feature Books: FX Option Pricing

Foreign exchange and option pricing, recommended reading.

Bonus Article: FX Vol Smiles - A Practical Construction Guide

Constructing the 10-delta and 25-delta wings starts with the three standard FX quotes: ATM volatility, risk reversal, and butterfly. The ATM vol gives the centre of the smile. The 25-delta butterfly gives the average of the call/put wings relative to ATM, and the 25-delta risk reversal gives the skew between the wings. Combining them yields the wing vols. The process is algebraically simple: RR shifts one wing up and the other down, and BF adds symmetric curvature.

To compute a 25-delta call volatility, take the ATM vol, add half the RR, and add the BF. For the 25-delta put, take the ATM vol, subtract half the RR, and add the BF. The 10-delta versions follow the exact same pattern. Once these vols are known, the final step is converting delta to strike.

FX uses forward-delta conventions; premium-adjusted delta is handled by subtracting the term d(Premium)/dS, which makes the hedge “net of premium”. This gives the strike that corresponds to each wing, allowing you to express the full smile in strike space.

Here is the simple set of formulas before the delta-to-strike step:

  • Vol(25D Call) = ATM + ½ RR(25D) + BF(25D)

  • Vol(25D Put) = ATM + ½ RR(25D) + BF(25D)

  • Vol(10D Call) = ATM + ½ RR(10D) + BF(10D)

  • Vol(10D Put) = ATM + ½ RR(10D) + BF(10D)

Afterwards, use premium-adjusted forward delta to solve for strike.

Below we show how to perform the calculations in python, including premium-adjusted delta.

# -*- coding: utf-8 -*-
"""
Currency pair: EUR/USD
- Spot rate S = 1.1500 USD per 1 EUR
- rd: domestic (USD) risk-free rate
- rf: foreign (EUR) risk-free rate
"""

import numpy as np
from math import log, sqrt, exp
from scipy.stats import norm
from scipy.optimize import root_scalar

def forward_delta_call(S, K, T, vol, rd, rf):
    """Standard forward delta for a call option"""
    F = S * exp((rd - rf) * T)
    d1 = (log(F / K) + 0.5 * vol**2 * T) / (vol * sqrt(T))
    return exp(-rf * T) * norm.cdf(d1)

def premium_adjusted_delta_call(S, K, T, vol, rd, rf):
    """Forward delta adjusted for premium"""
    F = S * exp((rd - rf) * T)
    d1 = (log(F / K) + 0.5 * vol**2 * T) / (vol * sqrt(T))
    d2 = d1 - vol * sqrt(T)
    forward_d = exp(-rf*T) * norm.cdf(d1)
    premium_sensitivity = forward_d * exp((rd - rf) * T)
    return forward_d - premium_sensitivity

def strike_from_delta(delta, S, T, vol, rd, rf, premium_adjust=False, call=True):
    """
    Solve for strike K corresponding to a given delta.
    If target delta is unachievable, returns the closest achievable delta.
    """
    def f(K):
        K = float(K)
        if K <= 0:
            return 1e10
        if call:
            d = premium_adjusted_delta_call(S, K, T, vol, rd, rf) if premium_adjust else forward_delta_call(S, K, T, vol, rd, rf)
        else:
            d = -forward_delta_call(S, K, T, vol, rd, rf)
        return d - delta

    K_min = 0.01
    K_max = 5*S

    f_min = f(K_min)
    f_max = f(K_max)

    if f_min * f_max > 0:
        # Target delta not achievable; pick closest
        d_min_val = premium_adjusted_delta_call(S, K_min, T, vol, rd, rf) if premium_adjust else forward_delta_call(S, K_min, T, vol, rd, rf)
        d_max_val = premium_adjusted_delta_call(S, K_max, T, vol, rd, rf) if premium_adjust else forward_delta_call(S, K_max, T, vol, rd, rf)
        closest_strike = K_min if abs(d_min_val - delta) < abs(d_max_val - delta) else K_max
        closest_delta = d_min_val if closest_strike == K_min else d_max_val
        print(f"Note: Target delta {delta:.5f} not achievable. Using closest achievable delta {closest_delta:.5f} at strike {closest_strike:.5f}")
        return closest_strike

    sol = root_scalar(f, bracket=[K_min, K_max], method='bisect', xtol=1e-12)
    return sol.root

def max_pa_delta(S, T, vol, rd, rf):
    """Compute maximum achievable premium-adjusted delta (usually near ATM)"""
    return premium_adjusted_delta_call(S, S, T, vol, rd, rf)

if __name__ == "__main__":
    # Market inputs
    S  = 1.1500   # Spot EUR/USD
    rd = 0.045    # USD risk-free rate (domestic)
    rf = 0.040    # EUR risk-free rate (foreign)
    T  = 90/365   # Time to expiry (years)
    vol = 0.12    # Volatility

    # Target deltas for the newsletter
    delta_25_call = 0.25
    delta_25_put  = -0.25

    # Compute maximum achievable PA delta
    achievable_delta_pa = max_pa_delta(S, T, vol, rd, rf)
    # For newsletter example, pick slightly below max to guarantee a valid strike
    delta_example_pa = min(delta_25_call, achievable_delta_pa*0.95)

    print("=== 25Δ Call ===")
    strike_call = strike_from_delta(delta_25_call, S, T, vol, rd, rf)
    print("Strike (Forward Delta): {:.5f}".format(strike_call))

    print("\n=== 25Δ Call (Premium-Adjusted) ===")
    strike_pa_call = strike_from_delta(delta_example_pa, S, T, vol, rd, rf, premium_adjust=True)
    print(f"Strike (PA Delta, delta={delta_example_pa:.5f}): {strike_pa_call:.5f}")

    print("\n=== 25Δ Put ===")
    strike_put = strike_from_delta(delta_25_put, S, T, vol, rd, rf, call=False)
    print("Strike (Forward Delta): {:.5f}".format(strike_put))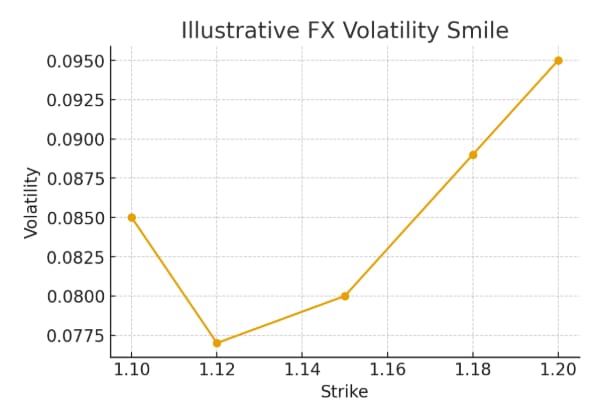

Keywords:
FX options, foreign exchange options, delta, forward delta, premium-adjusted delta, FX option trading, strikes, smile, volatility, risk-management, pricing, trading strategies

Feedback & Requests

I’d love your feedback to help shape future content to best serve your needs. You can reach me at [email protected]