Bond Markets & Algorithmic Adjoint Differentiation

About Me

About AlgoQuantHub

AlgoQuantHub includes the latest hands-on quant tutorials, videos and research, helping you bridge the gap between theory and real-world quant practice. All delivered by this newsletter! Each week I will deliver a targeted deep dive into a feature topic determined.

Subscribe to AlgoQuantHub’s Quant YouTube Channel!
Visit AlgoQuantHub’s Digital Download Store!

My goal is to use a wide variety of social media to make quantitative insights and complex concepts accessible to all. Premium content helps me support this effort, which I try to heavily discount for newsletter readers.

A Bond Market in Crisis?

Bond markets in 2025 have experienced significant turbulence, marked by rapid declines in bond prices and sharp rises in yields—especially for long-dated government bonds in the US, UK, and Japan. This volatility has been driven by a combination of factors:

• Rising Inflation Expectations: New tariffs and trade tensions have stoked fears of higher inflation, as companies like Walmart signal price hikes, and investors demand higher yields to compensate for increased risk.

• Fiscal and Debt Concerns: The US government’s large and growing debt—now exceeding $36 trillion—and concerns over budget deficits have made investors wary. The recent Moody’s downgrade of the US credit rating has further undermined confidence in US Treasuries, prompting some foreign investors to reduce holdings.

• Margin Calls and Leverage Unwinds: Hedge funds and leveraged investors, facing losses in equities and other markets, have been forced to sell liquid assets like bonds to meet margin calls. This has triggered a vicious cycle: as bond prices fall, yields rise, increasing borrowing costs for governments and corporations, and further pressuring fiscal positions.

• Geopolitical and Policy Uncertainty: The Trump administration’s “reciprocal tariffs” and unpredictable policy shifts have increased market uncertainty, reducing demand for US bonds and leading to a broader “sell America” trend.

• Global Ripple Effects: The sell-off has not been confined to the US. UK and Japanese long-term bond yields have surged to multi-decade highs, prompting emergency meetings and interventions by central banks.

The rapid decline in bond prices (and corresponding rise in yields) is thus a result of heightened risk aversion, fiscal stress, and policy uncertainty, compounded by technical factors like forced selling from leveraged positions.

Jamie Dimon, CEO of JPMorgan Chase, has publicly warned that excessive government spending and quantitative easing by the Federal Reserve are likely to lead to a “crisis” in the bond market. He emphasized that markets are underestimating the risks of inflation, stagflation, and credit spreads, and highlighted the potential for a sharp wake-up call as US Treasuries face their first monthly loss of the year amid mounting debt concerns.

https://www.pymnts.com/economy/2025/jamie-dimon-government-spending-will-cause-crisis-in-bond-market/

What is Algorithmic Adjoint Differentiation (AAD)?

Algorithmic Differentiation (AD), also known as automatic differentiation, is a mathematical, computer science technique for computing accurate sensitivities quickly. There are two main modes, namely tangent mode and adjoint mode. For many models, adjoint AD (AAD) can compute sensitivities 10s, 100s or even 1000s of times faster than numerical bumping and finite differences. AD operates directly on analytics and each line of code is differentiated. AD can be applied to a single trade or a portfolio of trades.

If for example we have a computer algorithm that computes y via multiple nested operations such as 𝑦 = h( g( f( x ) ) ) we could illustrate the series of operations as,

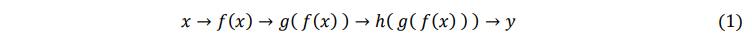
Working forwards from the input value x, we can compute the derivative of each operation and use the ‘chain rule’ to compute the total derivative dy/dx as follows

We could also work backwards from the output value y to arrive at the same result,

Furthermore AD can be used on systems of equations and matrices. Tangent mode works forward from the left and performs matrix-matrix multiplication followed by a final matrix-vector product,

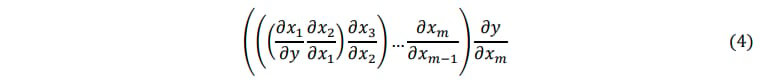
With adjoint mode we work backwards from the right, however now everything is matrix-vector products, which is much faster.

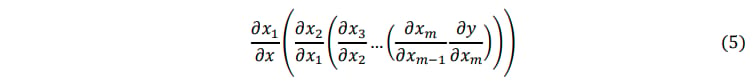
Tangent Mode
In tangent mode we differentiate code working forwards starting with the trade inputs and follow the natural order of the original program. This method computes price sensitivities to one input at a time and we must call the tangent method several times, once for each input parameter.

Dot Notation:
When using tangent mode ‘dot’ notation is used to denote derivatives being differentiated with respect to the function input. For example given y = f(x) then y dot would indicate 𝒚̇ = 𝒅𝒚/𝒅𝒙.

Consider the below simple function,

In tangent mode 𝒙̇ = 𝒅𝒙/𝒅𝒙 is specified as an input and used to enable/disable the tangent derivative calculation. Setting 𝒙̇ = 𝟏 in (equation 7) above enables the derivative calculation giving dy/dx = 4x, however when 𝒙̇ = 𝟎 we have dy/dx = 0.

Tangent Mode Example
Next let us consider how to apply tangent AD code to a simple function comprising of a series of simple incremental operations.

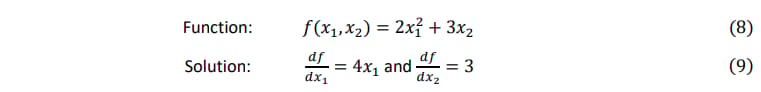
When x₁ = 2 and 𝑥₂ = 3 we have,

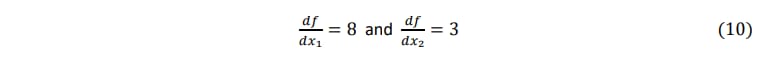
Let’s write this function in C++ code and implement (equation 8) as a series of operations spanning multiple lines of C++ code.

double function( double x1, double x2 )
{
   double a = x1*x1;   // Step 1: 𝑎 = 𝑥1^2
   double b = 2*a;     // Step 2: 𝑏 = 2𝑥1^2
   double c = x2;      // Step 3: 𝑐 = 𝑥2
   double d = 3*c;     // Step 4: 𝑑 = 3𝑥2
   double f = b + d;   // Step 5: 𝑓 = 2x1^2 + 3x2
   return f;
}

Run this code
To view and run this code see https://onlinegdb.com/kKqaS6hJT

Note the function f(x₁, x₂) takes two inputs, but we only have one f_dot derivative output. This means in tangent mode we can only get one derivative output at a time. So to compute the derivative of each input we would have to call the tangent method several times, once per input variable as follows,

// Input: x1 = 2, x2 = 3, x1_d = 1, x2_d = 0
// Output: 8
tangent(2.0, 3.0, 1.0, 0.0);

// Input: x1 = 2, x2 = 3, x1_d = 0, x2_d = 1 
// Output: 3
tangent(2.0, 3.0, 0.0, 1.0); 

As the function 𝑓(𝑥₁, 𝑥₂ ) = 2𝑥₁² + 3𝑥₂ with derivatives 𝑑𝑓/𝑑𝑥₁ = 4𝑥₁ and 𝑑𝑓/𝑑𝑥₂ = 3 as per (equations 8 and 9) then the returns the correct output values of 8 and 3 as given in (equation 10).

Adjoint Mode
When using adjoint mode we differentiate code in reverse order, starting with function outputs. Adjoint mode follows the reverse order of the original program, consequently we must compute the function value first ‘forward sweep’ and store the intermediate values before applying adjoint AD in reverse ‘back propagation’. This method shifts one function output at a time and generates derivatives exactly to machine precision for all price inputs in one go.

Bar Notation
Adjoint mode is computed using ‘bar’ notation for derivatives to denote the variable is to be differentiated with respect to the function input. For example given y = f(x) and working in reverse order gives 𝒙_bar = 𝒅𝒚/𝒅𝒙.

Once again let us consider same simple function from (equation 8),

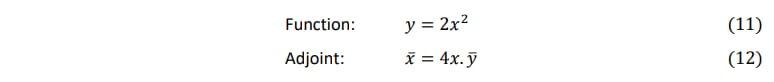
The adjoint bar notation in (equation 17) is equivalent to,

In adjoint mode 𝒚_bar = 𝒅𝒚/𝒅𝒚 is specified as an input and allows us to enable/disable the adjoint derivative calculation. Setting 𝒚_bar = 𝟏 in (equation 12) enables the derivative calculation giving dy/dx = 4x and when 𝒚_bar = 𝟎 we have dy/dx = 0.

Adjoint Mode Example
Next let us consider how to add to add adjoint AD code to the same simple function from (equation 8), requoted below for convenience.

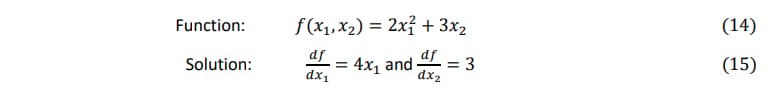
When 𝑥₁ = 2 and 𝑥₂ = 3 we have,

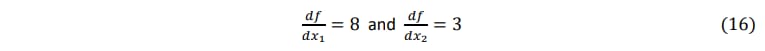
This function was implemented in (code block 1) above let’s apply adjoint AD (AAD) to this method, remembering that we are working backwards and in reverse. Consequently we must perform a forward sweep to evaluate the underlying function and store intermediate values for backpropagation and reverse calculation of derivatives as follows,

void adjoint( double x1, double x2, double f_bar )
{
   // Forward Sweep
   double a = x1*x1; // Step 1: 𝑎 = 𝑥1^2
   double b = 2*a;   // Step 2: 𝑏 = 2𝑥2^2
   double c = x2;    // Step 3: c = x2
   double d = 3*c;   // Step 4: 𝑑 = 3𝑥2
   double f = b + d; // Step 5: 𝑓 = 2𝑥1^2 + 3x2
   
   // Back Propagation
   double b_bar = f_bar;   // Step 5: b_bar = 1 (input variable)
   double d_bar = f_bar;   // Step 5: d_bar = 1 (input variable)
   double c_bar = 3*d_bar; // Step 4: c_bar = 3
   double x2_bar = c_bar;  // Step 3: x2_bar = 3 (𝑑𝑓/𝑑𝑥2 = 3)
   double a_bar = 2*b_bar; // Step 2: a_bar = 2
   double x1_bar = 2*x1*a_bar; // Step 1: x1_bar = 4𝑥1 (𝑑𝑓/𝑑𝑥1 = 4𝑥1)

   // Display Results
   std::cout << "df/dx1: " << x1_bar << std::endl;
   std::cout << "df/dx2: " << x2_bar << std::endl;
}

Run this code
To view and run this code see, https://onlinegdb.com/kKqaS6hJT

Note the function f(x₁, x₂) takes two inputs and in adjoint mode we capture both the x₁ and x₂ derivatives, namely x1_bar and x2_bar. This means that we capture a function’s derivatives to all inputs in one go and only need to call the adjoint method once as follows,

// Input: x1 = 3, x2 = 2, f_bar
// Output: 𝑑𝑓/𝑑𝑥1 = 8 and 𝑑𝑓/𝑑𝑥2 = 3
adjoint(2.0, 3.0, 1.0);

Conclusion
Algorithmic differentiation computes the exact derivatives of computer code to machine precision. There are two modes tangent (forward mode) and adjoint (backward mode). Adjoint mode computes all risks simultaneously!!! which is highly advantageous. Feel free to try it out and run the example code using the links above.

Featured Quant Video(s)

Subscribe to AlgoQuantHub’s Quant YouTube Channel!

In this video “Quant Models Unlocked” I discuss quant models for pricing and risk, looking at both the theory and the practise. I want to answer the question what tools and infrastructure do we need to build quant models and then give a practical example of quant models using interest yield curves and credit curves and show how they are calibrated and used to price Credit Default Swaps (CDS).

Featured Digital Download(s)

Visit AlgoQuantHub’s Digital Download Store!

My goal is to use a wide variety of social media to make quantitative insights and complex concepts accessible to all. Premium content helps me support this effort, which I try to heavily discount for newsletter readers.

This week we feature the Interest Rates & Fixed Income Training bundle, which contains Excel workbooks, PowerPoint and PDF training materials for interest rate and fixed income markets including the following,

• IR Markets Overview

• Interest Rate Swaps

• Cross Currency Swaps

• Credit Default Swaps

• Quanto Credit Default Swaps

• US Treasury Bonds

• Asset Swaps

• Bond Futures

This comprehensive training bundle covers the fundamentals of interest rate markets and provides step-by-step guidance on pricing key instruments, including interest rate swaps, cross-currency swaps, credit default swaps (CDS), and quanto CDS. You will also learn to price US Treasury bonds and accurately match bond prices and yields as quoted on major trading venues like Bloomberg. The course further explains asset swaps—enabling investors to finance bond purchases in a single transaction—and concludes with an overview of bond total return swaps, essential for creating synthetic Money Market and Bond ETFs.

Feedback & Requests

I’d love your feedback to help shape future content to best serve your needs, you can reach me at [email protected]